Which of the following equations has a graph in the xy-plane for which y is always greater than or equal to −1 ?
-
Solution
Since the square of any real number is nonnegative, every point on the graph of the quadratic equation y = (x − 2)2 in the xy-plane has a nonnegative y-coordinate. Thus, y ≥ 0 for every point on the graph. Therefore, the equation y = (x − 2)2 has a graph for which y is always greater than or equal to −1.
Choices A, B, and D are incorrect because the graph of each of these equations in the xy-plane has a y-intercept at (0, −2). Therefore, each of these equations contains at least one point where y is less than −1.
The graph of a line in the xy-plane has slope 2 and contains the point (1, 8). The graph of a second line passes through the points (1, 2) and (2, 1). If the two lines intersect at the point (a, b), what is the value of a + b?
-
Solution
Since the slope of the first line is 2, an equation of this line can be written in the form y = 2x + c, where c is the y-intercept of the line. Since the line contains the point (1, 8), one can substitute 1 for x and 8 for y in y = 2x + c, which gives 8 = 2(1) + c, or c = 6. Thus, an equation of the first line is y = 2x + 6. The slope of the second line is equal to \(\frac{1 − 2}{2 − 1}\) or −1.Thus, an equation of the second line can be written in the form y = −x + d,where d is the y-intercept of the line. Substituting 2 for x and 1 for y gives 1 = −2 + d, or d = 3. Thus, an equation of the second line is y = −x + 3.
Since a is the x-coordinate and b is the y-coordinate of the intersection point of the two lines, one can substitute a for x and b for y in the two equations,giving the system b = 2a + 6 and b = –a + 3. Thus, a can be found by solving the equation 2a + 6 = −a + 3, which gives a = −1. Finally, substituting −1 for a into the equation b = –a + 3 gives b = −(−1) + 3, or b = 4. Therefore, the value of a + b is 3.
Alternatively, since the second line passes through the points (1, 2) and (2, 1), an equation for the second line is x + y = 3. Thus, the intersection point of the first line and the second line, (a, b) lies on the line with equation x + y = 3. It follows that a + b = 3.
Choices A and C are incorrect and may result from finding the value of only a or b, but not calculating the value of a + b. Choice D is incorrect and may result from a computation error in finding equations of the two lines or in solving the resulting system of equations.
nA = 360
The measure A, in degrees, of an exterior angle of a regular polygon is related to the number of sides, n, of the polygon by the formula above. If the measure of an exterior angle of a regular polygon is greater than 50°, what is the greatest number of sides it can have?
-
Solution
The relationship between n and A is given by the equation nA = 360. Since n is the number of sides of a polygon, n must be a positive integer, and so nA = 360 can be rewritten as A = \(\frac{360}{n}\) . If the value of A is greater than 50, it follows that \(\frac{360}{n}\) > 50 is a true statement. Thus, 50n < 360, or n < \(\frac{360}{50}\) = 7.2. Since n must be an integer, the greatest possible value of n is 7.
Choices A and B are incorrect. These are possible values for n, the number of sides of a regular polygon, if A > 50, but neither is the greatest possible value of n. Choice D is incorrect. If A < 50, then n = 8 is the least possible value of n, the number of sides of a regular polygon. However, the question asks for the greatest possible value of n if A > 50, which is n = 7.
If \(\frac{x^{a^{2}}}{x^{b^{2}}}\) = x16, x > 1, and a b + =2, what is the value of a − b?
-
Solution
Since the numerator and denominator of \(\frac{x^{a^{2}}}{x^{b^{2}}}\) have a common base, it follows by the laws of exponents that this expression can be rewritten as \(x^{a^{2}-b^{2}}\). Thus, the equation \(\frac{x^{a^{2}}}{x^{b^{2}}}\)= 16 can be rewritten as \(x^{a^{2}-b^{2}}\)= x16. Because the equivalent expressions have the common base x, and x > 1, it follows that the exponents of the two expressions must also be equivalent. Hence, the equation a2 − b2 = 16 must be true. The left-hand side of this new equation is a difference of squares, and so it can be factored: (a + b)(a − b) = 16. It is given that (a + b) = 2; substituting 2 for the factor (a + b) gives 2(a − b) = 16. Finally, dividing both sides of 2(a − b) = 16 by 2 gives a − b = 8.
Choices B, C, and D are incorrect and may result from errors in applying the laws of exponents or errors in solving the equation a2 − b2 = 16.
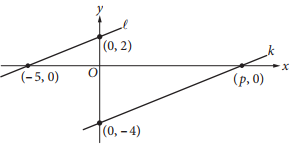
In the xy-plane above, line A is parallel to line k. What is the value of p ?
-
Solution
Since lines ℓ and k are parallel, the lines have the same slope. Line ℓ passes through the points (−5, 0) and (0, 2), so its slope is \(\frac{0 − 2}{−5 − 0}\), which is 2⁄5. The slope of line k must also be 2⁄5. Since line k has slope 2⁄5 and passes through the points (0, −4) and (p, 0), it follows that \(\frac{−4 − 0}{0 − p}\) = 2⁄5, or 4⁄p = 2⁄5.Multiplying each side of 4⁄p = 2⁄5 by 5p gives 20 = 2p, and therefore, p = 10.
Choices A, B, and C are incorrect and may result from conceptual or calculation errors.
If k > 0 and x = 7 in the equation above, what is the value of k ?
-
Solution

9a4 + 12a2b2 + 4b4
Which of the following is equivalent to the expression shown above?
-
Solution
If a polynomial expression is in the form (x)2 + 2(x)(y) + (y)2, then it is equivalent to (x + y)2. Because 9a4 + 12a2 b2 + 4b4 = (3a2 )2 + 2(3a2 )(2b2 ) + (2b2 )2 , it can be rewritten as (3a2 + 2b2 )2.
Choice B is incorrect. The expression (3a + 2b)4 is equivalent to the product (3a + 2b)(3a + 2b)(3a + 2b)(3a + 2b). This product will contain the term 4(3a)3 (2b) = 216a3 b. However, the given polynomial, 9a4 + 12a2 b2 + 4b4, does not contain the term 216a3 b. Therefore, 9a4 + 12a2 b2 + 4b4 ≠ (3a + 2b)4. Choice C is incorrect. The expression (9a2 + 4b2 )2 is equivalent to the product (9a2 + 4b2 )(9a2 + 4b2). This product will contain the term (9a2) (9a2) = 81a4. However, the given polynomial, 9a4 + 12a2 b2 + 4b4 , does not contain the term 81a4. Therefore, 9a4 + 12a2b2 + 4b4 ≠ (9a2 + 4b2)2.Choice D is incorrect. The expression (9a + 4b)4 is equivalent to the product(9a + 4b)(9a + 4b)(9a + 4b) (9a + 4b). This product will contain the term (9a)(9a)(9a)(9a) = 6,561a4. However, the given polynomial, 9a4 + 12a2b2 + 4b4 , does not contain the term 6,561a4. Therefore, 9a4 + 12a2 b2 + 4b4 ≠ (9a + 4b)4.
A landscaping company estimates the price of a job, in dollars, using the expression 60 + 12nh, where n is the number of landscapers who will be working and h is the total number of hours the job will take using n landscapers. Which of the following is the best interpretation of the number 12 in the expression?
-
Solution
The price of the job, in dollars, is calculated using the expression 60 + 12nh, where 60 is a fixed price and 12nh depends on the number of landscapers, n, working the job and the number of hours, h, the job takes those n landscapers. Since nh is the total number of hours of work done when n landscapers work h hours, the cost of the job increases by $12 for each hour a landscaper works. Therefore, of the choices given, the best interpretation of the number 12 is that the company charges $12 per hour for each landscaper.
Choice B is incorrect because the number of landscapers that will work each job is represented by n in the equation, not by the number 12. Choice C is incorrect because the price of the job increases by 12n dollars each hour, which will not be equal to 12 dollars unless n = 1. Choice D is incorrect because the total number of hours each landscaper works is equal to h. The number of hours each landscaper works in a day is not provided.
x + y = 0
3x − 2y = 10
Which of the following ordered pairs (x, y) satisfies the system of equations above?
-
Solution
Multiplying each side of x + y = 0 by 2 gives 2x + 2y = 0.Then, adding the corresponding sides of 2x + 2y = 0 and 3x − 2y = 10 gives 5x = 10. Dividing each side of 5x = 10 by 5 gives x = 2. Finally, substituting 2 for x in x + y = 0 gives 2 + y = 0, or y = −2. Therefore, the solution to the given system of equations is (2, −2).
Alternatively, the equation x + y = 0 can be rewritten as x = −y, and substituting x for −y in 3x − 2y = 10 gives 5x = 10, or x = 2. The value of y can then be found in the same way as before.
Choices A, C, and D are incorrect because when the given values of x and y are substituted into x + y = 0 and 3x − 2y = 10, either one or both of the equations are not true. These answers may result from sign errors or other computational errors.
If 5x + 6 = 10 , what is the value of 10x + 3?
-
Solution
Subtracting 6 from each side of 5x + 6 = 10 yields 5x = 4.Dividing both sides of 5x = 4 by 5 yields x =4⁄5. The value of x can now be substituted into the expression 10x + 3, giving 10 (4⁄5) + 3 = 11.
Alternatively, the expression 10x + 3 can be rewritten as 2(5x + 6) − 9, and 10 can be substituted for 5x + 6, giving 2(10) − 9 = 11.
Choices A, B, and D are incorrect. Each of these choices leads to 5x + 6 ≠ 10, contradicting the given equation, 5x + 6 = 10. For example, choice A is incorrect because if the value of 10x + 3 were 4, then it would follow that x = 0.1, and the value of 5x + 6 would be 6.5, not 10.
