If a = 5√2 and 2a = √2x , what is the value of x ?
-
Solution
The correct answer is 100. Since a = 5√2 , one can substitute 5√2 for a in 2a = √2 x, giving 10√2 = √2 x. Squaring each side of 10√2 = √2 x gives (10√2)2 = (√2x)2, which simplifies to (10)2 (√2)2 = (√2x)2, or 200 = 2x. This gives x = 100. Checking x = 100 in the original equation gives 2(5√2) = \sqrt{(2)(100)},which is true since 2(5√2 ) = 10√2 and \sqrt{(2)(100)} = (√2)(\sqrt{100}) = 10√2.
In a right triangle, one angle measures x°, where sin x° = 4⁄5. What is cos(90° − x°)?
-
Solution
The correct answer is 4⁄5 or 0.8. By the complementary angle relationship for sine and cosine, sin(x°) = cos(90° − x°). Therefore, cos(90° − x°) = 4⁄5.Either the fraction 4⁄5 or its decimal equivalent, 0.8, may be gridded as the correct answer.
Alternatively, one can construct a right triangle that has an angle of measure x° such that sin(x°) = 4⁄5, as shown in the figure below, where sin(x°) is equal to the ratio of the opposite side to the hypotenuse, or 4⁄5.

Since two of the angles of the triangle are of measure x° and 90°, the third angle must have the measure 180° − 90° − x° = 90° − x°. From the figure, cos(90° − x°), which is equal to the ratio of the adjacent side to the hypotenuse,is also 4⁄5.
x + y = −9
x + 2y = −25
According to the system of equations above, what is the value of x ?
-
Solution
The correct answer is 7. Subtracting the left and right sides of x + y = −9 from the corresponding sides of x + 2y = −25 gives (x + 2y) − (x + y) = −25 − (−9), which is equivalent to y = −16. Substituting −16 for y in x + y = −9 gives x + (−16) = −9, which is equivalent to x = −9 − (−16) = 7.
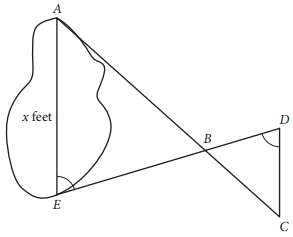
A summer camp counselor wants to find a length, x, in feet, across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet, and 800 feet, respectively. Segments AC and DE intersect at B, and ∠AEB and ∠CDB have the same measure. What is the value of x ?
-
Solution
The correct answer is 1600. It is given that ∠AEB and ∠CDB have the same measure. Since ∠ABE and ∠CBD are vertical angles, they have the same measure. Therefore, triangle EAB is similar to triangle DCB because the triangles have two pairs of congruent corresponding angles (angleangle criterion for similarity of triangles). Since the triangles are similar, the corresponding sides are in the same proportion; thus \frac{CD}{x}=\frac{BD}{EB}. Substituting the given values of 800 for CD, 700 for BD, and 1400 for EB in \frac{CD}{x}=\frac{BD}{EB} gives \frac{800}{x}=\frac{700}{1400}. Therefore, x =\frac{(800)(1400)}{700} = 1600.
If t > 0 and t2 − 4 = 0, what is the value of t ?
-
Solution
The correct answer is 2. To solve for t, factor the left side of t2 − 4 = 0, giving (t − 2)(t + 2) = 0. Therefore, either t − 2 = 0 or t + 2 = 0. If t − 2 = 0, then t = 2, and if t + 2 = 0, then t = −2. Since it is given that t > 0, the value of t must be 2.
Another way to solve for t is to add 4 to both sides of t2 − 4 = 0, giving t2 = 4. Then, taking the square root of the left and the right side of the equation gives t = ±√4 = ±2. Since it is given that t > 0, the value of t must be 2.
If (ax + 2)(bx + 7) = 15x2 + cx + 14 for all values of x, and a + b=8, what are the two possible values for c ?
-
Solution
One can find the possible values of a and b in (ax + 2)(bx + 7) by using the given equation a + b = 8 and finding another equation that relates the variables a and b. Since (ax + 2)(bx + 7) = 15x2 + cx + 14, one can expand the left side of the equation to obtain abx2 + 7ax + 2bx + 14 = 15x2 + cx + 14. Since ab is the coefficient of x2 on the left side of the equation and 15 is the coefficient of x2 on the right side of the equation, it must be true that ab = 15. Since a + b = 8, it follows that b = 8 − a. Thus, ab = 15 can be rewritten as a(8 − a) = 15, which in turn can be rewritten as a2 − 8a + 15 = 0. Factoring gives (a − 3)(a − 5) = 0. Thus, either a = 3 and b = 5, or a = 5 and b = 3. If a = 3 and b = 5, then (ax + 2) (bx + 7) = (3x + 2)(5x + 7) = 15x2 + 31x + 14. Thus, one of the possible values of c is 31. If a = 5 and b = 3, then (ax + 2)(bx + 7) = (5x + 2)(3x + 7) = 15x2 + 41x + 14. Thus, another possible value for c is 41. Therefore, the two possible values for c are 31 and 41.
Choice A is incorrect; the numbers 3 and 5 are possible values for a and b, but not possible values for c. Choice B is incorrect; if a = 5 and b = 3, then 6 and 35 are the coefficients of x when the expression (5x + 2)(3x + 7) is expanded as 15x2 + 35x + 6x + 14. However, when the coefficients of x are 6 and 35, the value of c is 41 and not 6 and 35. Choice C is incorrect; if a = 3 and b = 5, then 10 and 21 are the coefficients of x when the expression (3x + 2)(5x + 7) is expanded as 15x2 + 21x + 10x + 14. However, when the coefficients of x are 10 and 21, the value of c is 31 and not 10 and 21.
If 3x − y= 12, what is the value of \frac{8^{x}}{2^{y}}?
-
Solution
One approach is to express \frac{8^{x}}{2^{y}}so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting 23 for 8 in the numerator of \frac{8^{x}}{2^{y}} gives \frac{(2^{3})^{x}}{2^{y}} , which can be rewritten as \frac{2^{3x}}{2^{y}}. Since the numerator and denominator of \frac{2^{3x}}{2^{y}} have a common base, this expression can be rewritten as 23x−y. It is given that 3x − y = 12, so one can substitute 12 for the exponent, 3x − y, giving that the expression \frac{2^{x}}{2^{y}} is equal to 212.
Choices B and C are incorrect because they are not equal to 212. Choice D is incorrect because the value of \frac{8^{x}}{2^{y}} can be determined.
If x > 3, which of the following is equivalent to \frac{1}{\frac{1}{x+2}+\frac{1}{x+3}}?
-
Solution
To rewrite \frac{1}{\frac{1}{x+2}+\frac{1}{x+3}}, multiply by \frac{(x + 2)(x + 3)}{(x + 2)(x + 3)}.This results in the expression \frac{(x + 2)(x + 3)}{(x + 3) + (x + 2)}, which is equivalent to the expression in choice B.
Choices A, C, and D are incorrect and could be the result of common algebraic errors that arise while manipulating a complex fraction.
A line in the xy-plane passes through the origin and has a slope of 1⁄7. Which of the following points lies on the line?
-
Solution
Determine the equation of the line to find the relationship between the x- and y-coordinates of points on the line. All lines through the origin are of the form y = mx, so the equation is y = 1⁄7 x. A point lies on the line if and only if its y-coordinate is 1⁄7 of its x-coordinate. Of the given choices, only choice D, (14, 2), satisfies this condition: 2 = 1⁄7(14).
Choice A is incorrect because the line determined by the origin (0, 0) and (0, 7) is the vertical line with equation x = 0; that is, the y-axis. The slope of the y-axis is undefined, not 1⁄7. Therefore, the point (0, 7) does not lie on the line that passes the origin and has slope 1⁄7. Choices B and C are incorrect because neither of the ordered pairs has a y-coordinate that is 1⁄7 the value of the x-coordinate.
b = 2.35 + 0.25x
c = 1.75 + 0.40x
In the equations above, b and c represent the price per pound, in dollars, of beef and chicken, respectively, x weeks after July 1 during last summer. What was the price per pound of beef when it was equal to the price per pound of chicken?
-
Solution
To determine the price per pound of beef when it was equal to the price per pound of chicken, determine the value of x (the number of weeks after July 1) when the two prices were equal. The prices were equal when b = c; that is, when 2.35 + 0.25x = 1.75 + 0.40x. This last equation is equivalent to 0.60 = 0.15x, and so x = \frac{0.60}{0.15}= 4. Then to determine b, the price per pound of beef, substitute 4 for x in b = 2.35 + 0.25x, which gives b = 2.35 + 0.25(4) = 3.35 dollars per pound.
Choice A is incorrect. It results from using the value 1, not 4, for x in b = 2.35 + 0.25x. Choice B is incorrect. It results from using the value 2, not 4, for x in b = 2.35 + 0.25x. Choice C is incorrect. It results from using the value 3, not 4, for x in c = 1.75 + 0.40x.
